This section describes the mathematical analysis of the family growth that I used to try to get an estimate of the possible size of the family today. I used logarithmic linear regression analysis to project an estimate of the number of members in each generation. Note that this is not an estimate of the number of people alive today.
In the first place, members of more than one generation will be alive at any point in time. And in each generation with living members, some will have already died and some will be as yet unborn. The rule of thumb states that there will be one generation every 33 years. That is three generations per century. But most women reach child-bearing age around 15 or 16, and some even earlier. So it certainly possible that some lines could have up to six generations per century. The effect of this is that the spread of generations with members among living will increase in time.
So the numbers of people in each generation will give you an overall estimate of how the numbers are increasing, but without the actual birth and death dates of the individuals it is not possible to specify exactly how many from each generation will be alive at any time. The fact that Allen missed some members and also that some members will not be descendants of Harmon Hendrick will lower the counts.
The following table contains the counts of entries in Allen's book by generation. Bear in mind that these are numbers of people who have been born only; there are no figures for people who are currently alive or who have died. There could easily be members from the 8th and almost certainly from the 9th who are still living today.
| Generation | Members |
| 1 | 1 |
| 2 | 9 |
| 3 | 21 |
| 4 | 31 |
| 5 | 73 |
| 6 | 251 |
| 7 | 333 |
| 8 | 186 |
| 9 | 17 |
Table 1 - Counts From Allen's Book
This data has been displayed in the bar graph in Figure 1, below. It is known that population increase is an exponential function. We expect the curve to be steadily curving upward; in fact this upward curvature breaks after the sixth generation; the curve would have to turn in the opposite direction in order to include the top of the seventh bar. And it clearly turns sharply downward after this. So I used the first six generations in the regression calculation to estimate the growth from the seventh generation onward.
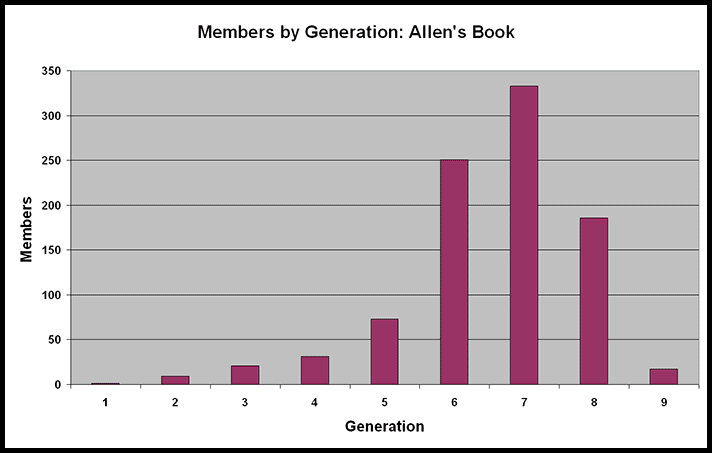
Figure 1. Generation Distribution From Allen's Book
Table 2 gives the calculated results based on estimates from the first six generations:
| Generation | Estimated Members |
| 1 | 1 |
| 2 | 5 |
| 3 | 13 |
| 4 | 36 |
| 5 | 95 |
| 6 | 253 |
| 7 | 432 |
| 8 | 953 |
| 9 | 2100 |
| 10 | 4627 |
| 11 | 10199 |
| 12 | 22477 |
Table 2. Calculated Number of People in Each Generation
It is obvious that there were probably a hundred or so members from the seventh generation who were not even born at the time Allen completed his survey. And the eighth generation by itself could have been more numerous that the total number of people in Allen's book (927!)
These numbers seem to be realistic and perhaps even a little low. From the slope of the logarithmic regression curve we can calculate that each person, on average, had 2.33 children. Although ~50% of these are women, so their children won't appear in the counts, families were generally larger then. That doesn't seem too out of line with today's statistical average of 2.46 children per family. But other demographic factors such as birth control and the tendency for people to want smaller families may be at work.
There are too many unknowns to make an accurate estimate. Nevertheless, it doesn't seem too far out of line to me to say that there are probably several thousand family members in all. Figure 2 below shows the projections through the 12th generation plotted alongside the numbers from Allen's book (in red.) The estimate for the 14th generation (not plotted here) was over 100,000!

Figure 2. Comparison of Projections with Allen's Data
For those of you who can handle the math, this can be easily calculated using a Microsoft EXCEL spreadsheet:
Put the generation numbers in column A: 1, 2, ..., 14
Count the people in generations 1 - 9 in column B (Table 1, above) in Allen's book
Generate Figure 1 using the first 9 rows of A and B.
Calculate the natural logarithm LN() of the first 6 rows of column B and put them in column C.
Using as data the first six rows of columns A and C, and use the FORECAST() function to calculate the natural logarithm of the number of people for generations 1, 2, ... , 14 and place these numbers in column D.
Calculate the exponential EXP() of each logarithm in column D, round it off to zero decimal places {ROUND()}, and place the results in column E (Table 2.)
Column A contains the generation numbers, the first 9 lines of column B contains the counts from Allen's book, and the first 14 lines of column E contains the estimated size of the generation. Use this data to create the Figure 2 graph.
Use the SLOPE() function and then exponentiate the result EXP() to arrive at the average number of children per person.
Copyrightę 2007 by James P. Rosenkrans, IV. All rights reserved.